szöggyorsulással
Így a számértéke szöggyorsulás adott időben egyenlő egy első deriváltja a szögsebesség vagy a második származékot a forgásszög idővel.
A dimenziója szöggyorsulása a $ 1 / T ^ 2 $ ($ 1 / idő ^ 2 $); a mértékegység általánosan használt $ rad / s ^ 2 $, vagy, más szóval, $ 1 / s ^ 2 $ $ (a ^) $.
Ha a modul szögsebesség idővel növekszik, a test forgását is hívják felgyorsult, és ha csökken késik. Könnyen belátható, hogy a forgatás kell gyorsítani, ha az értéke $ \ omega $ és $ \ varepsilon $ azonos jeleket, és késleltetett - ha különböző jeleket.
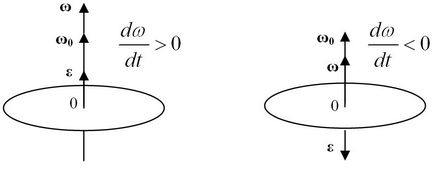
1. ábra A vektor a szöggyorsulás
A szöggyorsulással a test is képviselteti magát egy vektor $ \ overrightarrow = \ frac> $. irányította a forgási tengely mentén. Irányban $ \ overrightarrow $ egybeesik irányába $ \ $ overrightarrow, amikor a test sebességgel forgatni (1a ábra), és egymással szemben $ \ overrightarrow \ $ lassú forgatás közben (1b ábra).
Ha a szöggyorsulás a test egész mozgás állandó marad ($$ = const), az elforgatás nevezzük ravnoperemennym. Találunk ravnoperemennogo jog forgás, feltételezve, hogy a kezdeti időben $ t_0 $ = $$ $$ szög 0 és a szögsebesség 0 $$ $$ = (0 $$ - kezdeti szögsebesség).
Formula $ \ varepsilon = \ frac = \ dot = \ ddot $ van d $ \ omega $ = $ \ varepsilon $ dt. Integrálása a bal oldalon a tartományban $ \ omega_0 $ és $ \ omega $, és a jobb oldalon - a 0-tól t találunk:
$ \ Omega $ = $ \ omega_0 $ + $ \ varepsilon $ t, d $ \ varphi $ = $ \ omega $ 0DT + $ \ varepsilon TDT $.
Ha az érték a $ \ omega $ és $ \ varepsilon $ ugyanaz az előjele, akkor a forgatás lesz egyenletesen gyorsuló, és ha ettől eltérő - ravnozamedlennym.
A szöggyorsulás társított teljes és érintőleges. Pontokat egyenletesen forgó egy R sugarú kör, $ a = _ \ varepsilon R $. Tekintettel arra, hogy a gyorsulás szögsebességet $ a_n = ^ 2R $, hogy megkapjuk a teljes gyorsulás: $ a = \ sqrt + a ^ 2_n> = R \ sqrt ^ 2 + 4 ^> $. Abban az esetben, egyenletesen gyorsuló mozgás $ \ omega = \ varepsilon t $, $ a_n = ^ 2R = ^ 2t ^ 2R $, $ a = R \ sqrt ^ 2 + \ varepsilon> ^ 4t ^ 4> = R \ varepsilon \ sqrt ^ 2t * 4> $
A 2. ábra mutatja a forgásirányt a giroszkóp (giroszkóp) és jelzi a szögsebesség növekszik vagy csökken. Határozza meg a számát az ábra, amely megfelelően jelzik az irányt a szöggyorsulás.
Pszeudo szögsebesség összefügg a forgási iránya jobb kéz szabályt (jobb oldali csavart). Ábra. 2.1 és ábra. 2.3 azt felfelé irányul ábra. 2.2 és ábra. 2.4 - lefelé.
A növekvő a szögsebesség növekmény, és így a szöggyorsulás vektort egybeessen a szögsebesség-vektora (1. és 4. ábra). A csökkentésével szögsebesség növekmény, és ennek megfelelően, a szöggyorsulás vektor ellentétes a vektor a szögsebesség (2. ábra és a 3. ábra). Következésképpen, minden a számok az irányt a szöggyorsulással helyes.
A anyag végighalad egy R sugarú kör úgy, hogy a függőség a forgatási szög a időt a következő egyenlet adja $$ = $$ t3. Keresse meg a teljes gyorsulás a lényeg, mint az idő függvényében.
Keresse meg a szögsebesség és szöggyorsulásakor a lényeg:
\ [\ Omega = \ frac = 3 \ alpha t ^ 2 ;; \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ varepsilon = 6 \ alpha t \]